It is important to keep in mind that a knife throw happens instinctively, without thinking, much like walking or riding a bike. You must not try to think of the throw! Helpful notions like "release when the knife is pointing exactly at the target" are necessary to learn the motion sequence, but your brain will automatically adjust to release the knife in the right moment (a little earlier). Another example for this is "holding higher". Here too, you just can`t explain what exactly you change in your throw.
The following explanations are just for the sake of completeness, for those who are curious to learn about the physics involved in a knife throw. Michael, thank you very much for the drawings and your thoughts on the topic.
This page deals only with the standard overhand knife throw. For other throwing styles, such as no spin knife throwing, other factors become the relevant ones.
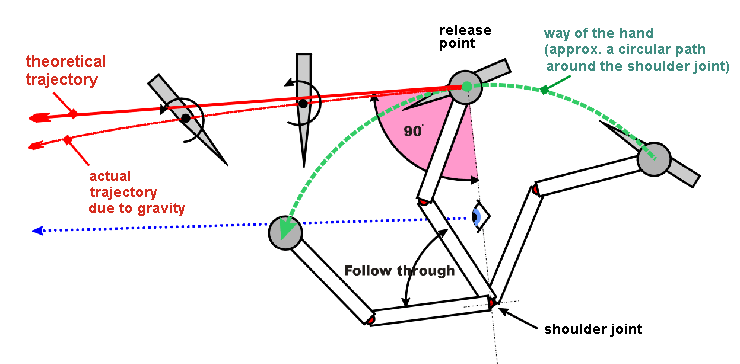
If someone is new to throwing, he will always be told to release the knife when it points exactly at the target. This advice, which does well as a helping notion, is given by many books as well. But in reality, the knife is released earlier.
Describing it with regard to physics, the following happens: The hand makes about a circular motion around the shoulder joint. The movements in the elbow joint just change the radius of the circle and will be ignored.
Once released, the knife will fly on tangentially to the circular path (see the pink 90° angle of the trajectory to the radius, and the picture; the knife is gripped by the blade!). Perhaps some of you remember the experiment in physics at school, when the teacher swung a weight on a string around his head and then let go?
If you were to release the knife exactly when pointing to the target (blue line), it would fly straight to the ground. Rather, it must be released when the tangent of the circular path of the swing points exactly at the target (upper red line), or better a little earlier, because the ideal tangential trajectory will be affected by gravity (lower red line).
In the very moment when releasing the knife, it will be about perpendicular to the ground, then start to turn. The arm will go on in his downward swing (follow through).
 In this case, personal perception and reality diverge. At first, based on my experience, I could not believe I release the knife that early. But it has to be that way, physics proves it, and some other things: when reviewing the slow motion sequences in his video, David Adamovich discovered that his knives leave the hand when being perpendicular to the ground, and Tim Valentine came to the same conclusion after doing some video analysis (he took this fact into account when writing his
In this case, personal perception and reality diverge. At first, based on my experience, I could not believe I release the knife that early. But it has to be that way, physics proves it, and some other things: when reviewing the slow motion sequences in his video, David Adamovich discovered that his knives leave the hand when being perpendicular to the ground, and Tim Valentine came to the same conclusion after doing some video analysis (he took this fact into account when writing his ![]() distance-turns-formula; 2 turns really are 2¼). Below, there are some photos taken immediately after the release of the knife, at the Thrower Meeting 2002 in Müncheberg (thank you, press photographer Johann Müller from Döbberin).
distance-turns-formula; 2 turns really are 2¼). Below, there are some photos taken immediately after the release of the knife, at the Thrower Meeting 2002 in Müncheberg (thank you, press photographer Johann Müller from Döbberin).
 |
 |
 |
 |
As mentioned above, the throwing movement follows a circular path around the shoulder joint. During the throwing movement, the knife changes its angle to the ground (Δφ), like a watch hand. The value of the changed angle per time is called ![]() angular velocity ω in physics. After releasing the knife, it will fly forward and continue to rotate around its center of gravity with the same angular velocity it had during the throwing movement. At the end of the throwing movement, the tip of the blade goes down (if you are holding it at the handle for the throw, that is), and so it will during the flight: tip going down, handle coming up. Thus, if your knife reaches the target with the handle pointing up, it has turned too much, and you must go nearer to the target to allow less time for rotation.
angular velocity ω in physics. After releasing the knife, it will fly forward and continue to rotate around its center of gravity with the same angular velocity it had during the throwing movement. At the end of the throwing movement, the tip of the blade goes down (if you are holding it at the handle for the throw, that is), and so it will during the flight: tip going down, handle coming up. Thus, if your knife reaches the target with the handle pointing up, it has turned too much, and you must go nearer to the target to allow less time for rotation.
The rotation of the knife around its center of gravity depends on how fast you are changing the angle of the knife (=Δφ) during the throwing movement. Now, if you do minimise the circle of the movement by not extending your arm, keeping it bent, throwing with usual speed will result in a faster rotation of the knife (higher ω), because in the smaller circle it takes less time to move the knife for a certain angle. Accordingly, you can also slow down the rotation using a larger circle, extending your arm. This is also accomplished by the technique of "leaning in", where you stretch the throwing movement towards the target, making it into an oblong oval. With respect to the angular velocity, this oval acts like a larger circle (→ slower rotation).
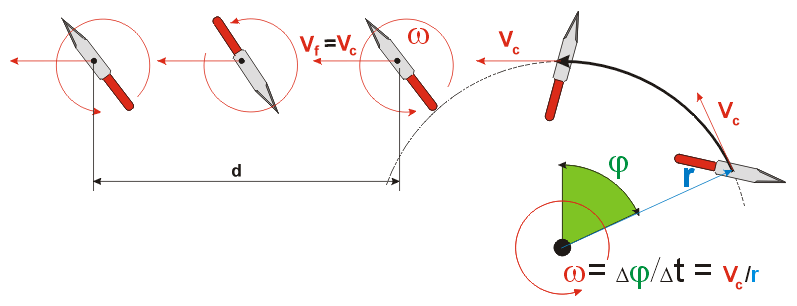
It is very interesting to note that the velocity of your throw has no impact on the distance the knife will travel during one full rotation!
Proof: The angular velocity ω (angle per time t) can be measured in radian, its unit is then 2π / t . The distance d the knife travels while completing one full rotation is his forward velocity Vf multiplied by the time needed to complete the rotation:
d = Vf ∙ (2π / ω) (formula 1)
The forward velocity Vf of the knife equals its circumferential velocity Vc at the moment of release. Vc is the part of the circular arc (with the radius r measured from the shoulder joint to the center of gravity of the knife) that is covered by the knife per time unit, and with ω already being in radian, the formula is (circumference equals r ∙ 2π):
Vf = Vc = r ∙ ω (formula 2)
Inserting formula 2 into formula 1 yields:
d = r ∙ 2π (formula 3)
The distance d which the knife travels during one full rotation hence only depends on the radius of the throwing movement, not on the force or speed of the throw! ∎
The last formula also explains why axes (and large knives) travel longer distances during one full turn: their center of gravity is well away from the hand, making the radius r of the circular throwing movement bigger.
The formula d = r ∙ 2π (formula 3) derived above is of little use practically, since the radius r is not known. The throwing movement is not an exact circle, but a bent curve, and the relevant radius r is the one of the curve at the moment of release. The conclusion that the parameter d (traveled way/full rotation) only depends on the distance (radius r) of the shoulder joint to the center of gravity of the knife remains true (presuming that the throwing movement itself is not changed, of course).
Because the arm length of the thrower remains constant, and only the radius changes with different throwing devices, it is possible to empirically determine the parameter d for throwing devices of different length. Experiments yielded the following diagram:
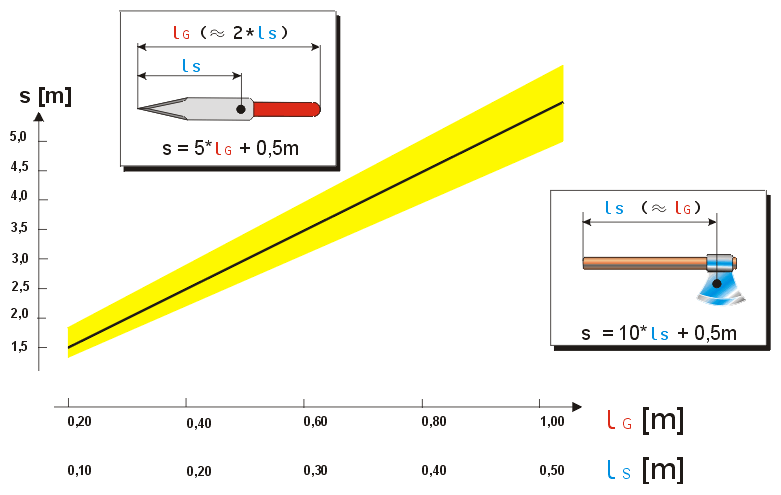
Here, lg is the whole (general) length of a knife, ls is the distance or location of the center of mass, which will be assumed to be at lg/2, because well balanced throwing knives have their center of gravity in the middle. With axes, the center of gravity is nearly exactly at the end of the handle, hence we set ls equal to lg. Therefore, the lg axis in the diagram is for the knives, ls for the axes.
Example:A knife with a length of 30cm (lg = 0.3m) would travel around 2m while completing a full turn. An axe with a handle length of 30cm (ls = 0.3m) would need about 3.5m for that according to the diagram. These values are true for a normal throw using the hammer grip. Due to different grip variations and other factors, the real values can scatter around the ones given (yellow area in the diagram).
Knife throwers know that they can slow down the rotation of a knife by taking more of it into the hand, holding it more towards the middle. This results from the fact that the knife needs more time to clear the hand after the release, whilst the hand continues to travel downwards, pushing onto the handle. This slows down the rotation, which normally would have the handle going up. The technique of throwing the knife with the thumb on its spine slows down the rotation for the same reason.
Another alteration of the grip does slow down the rotation: do not hold the knife so that it is a straight extension of your horizontally outstretched forearm, but bend it slightly back up. After being released, the knife can now not easily slide out of the hand, but has to work against the front fingers, tumbling over them, thus adding spin.
To see what the rotation of a thrown knife looks like in flight, see the following video of a full turn throw.
(Slow-motion video at ¼ speed, provided by Cleif Ludwig.)
The speed of a thrown knife depends of course on the power of the thrower and on the throwing technique employed. There are reliable experiments which clock the speed of a ball thrown by a handball player at up to 120 km/h. But those were professionals.

David Adamovich made an ![]() experiment to determine the speed of throwing knives: In front of a background that had vertical lines every 3 inches, a knife was thrown with "normal" speed across a distance of 3.4m. The flight was filmed with 60 frames/second (KnifeThrowing.info has seen the video), and the speed of the knife calculated as being around 50km/h. Do note that the knife turns and hence for the impact on the target the rotational speed would have to be added.
experiment to determine the speed of throwing knives: In front of a background that had vertical lines every 3 inches, a knife was thrown with "normal" speed across a distance of 3.4m. The flight was filmed with 60 frames/second (KnifeThrowing.info has seen the video), and the speed of the knife calculated as being around 50km/h. Do note that the knife turns and hence for the impact on the target the rotational speed would have to be added.
A very similar experiment was done by a TV team reporting on our Big Throwers Meeting 2007. (The somewhat lurid report by German national TV chain Pro7/Galileo can be ![]() viewed here.) The results are very accurate, since the two test-throwers were filmed with a high-speed camera that could record several hundred pictures per second. The knife speeds of 55 km/h and 61 km/h reported were somewhat higher the one given by Adamovich. However, the faster speed was observed with a very fast thrower (Gregor Paprocki) who throws all his body towards accelerating his bayonet.
viewed here.) The results are very accurate, since the two test-throwers were filmed with a high-speed camera that could record several hundred pictures per second. The knife speeds of 55 km/h and 61 km/h reported were somewhat higher the one given by Adamovich. However, the faster speed was observed with a very fast thrower (Gregor Paprocki) who throws all his body towards accelerating his bayonet.
Knife throwers will most probably throw less hard, hence slower, at short distances, than they would for long ones. This is partly so due to the fact that they fear the bounces of the knives from the target, which can be dangerous at short range. Long throws (> 6m) are done harder, keeping the arch of the trajectory flat due to increased speed. The hope is achieving a higher accuracy, because one can focus better on the target. But as already shown, this is of no help as the knife is not on the line eye-target on release.
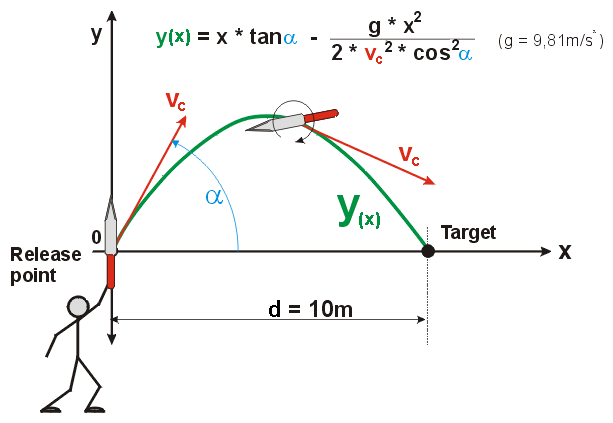
The slower the speed of the throw, the higher the arch of the trajectory must be, hence the real distance traveled to the target will increase (see Figure 1, green curve). As already shown, the distance a knife travels during one full turn does not depend on the initial speed of the throw. So, in theory one should be able to control any over- or underspinning of the knife as it hits the target (as higher initial speed results in a shorter distance traveled to the target).
In reality, this would only be the case if the distance the knife really traveled to the target (Figure 1, green curve) were significantly different to the distance to the target (Figure 1, distance d). This can be calculated using the formula for the trajectory of an angular throw (see Figure 1, formula y(x) ). A graphical representation of the results is shown in Figure 2:
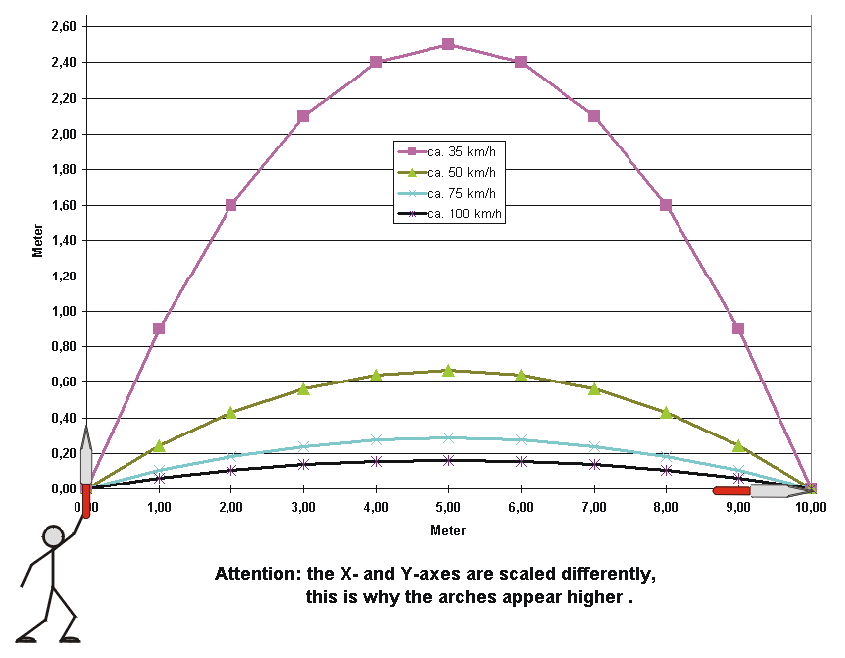
Four different throws with initial speeds Vc between 35km/h and 100km/h were examined, the formula for the trajectory of the knife (see Figure 1, formula y(x) ) being used to calculate the corresponding angles α of the throw. The angle of 45 degrees is a special case, it allows to achieve the furthest throws, a knife (or any other object) thrown at this angle with a speed of 35km/h will just about make it to the target. The distance d to the target has been set as 10m, the target point is on the same level as the point of release (so we are looking for y = 0). The following is a chart with the speed of the throws, corresponding angles and corresponding real distances traveled on the arch during the flight:
| Initial speed [km/h] |
Angle of throw [degree] |
Real distance on arch [m] |
|---|---|---|
| 35,66 | 45,00 | 11,47 |
| 50,43 | 15,00 | 10,12 |
| 75,18 | 6,50 | 10,02 |
| 99,09 | 3,72 | 10,01 |
Evidently, the difference between the real distance to the target (d = 10m) and the real distance traveled by the knife on the arch is rather low in the range of 50km/h to 100km/h. Only for very weak throws (35km/h) one can see a significant influence of the speed.
Conclusion: Even for long distance throws one should stick to a relaxed throw.
To see all the phyics in action, have a look at the beautiful trajectory of an axe, thrown from somewhere just beyond the 12m mark.